Vektörler Nedir
Vektörler Ne Demek? Vektörler Nedir Kısaca? Vektörler Ne Demektir? Vektörler Hakkında Bilgi? Vektörler Kısaca Nedir?
Vektörler Ne Demek, Skaler Büyüklük Sayı ve birim kullanılarak belirtilebilen büyüklüklere skaler büyüklük denir. Örneğin “5Kg” değeri skaler bir büyüklüktür Vektörel Büyüklük Sayı ve birime ek olarak bir dogrultu ve yöne sahip olan büyüklüklere vektörel büyüklük ismi verilir. Örneğin fizikte hizlar vektörlerle ifade edilir. Yönü, dogrultusu ve degeri ayni olan vektörlere “es vektörler” denir.Yönleri ters dogrultulari ve degerleri ayni olan vektörlere “zit vektörler” denir.Vektörel bir ifadenin skaler bir ifade ile çarpimi yada bölümü, vektörel bir büyüklüktür.iki vektörün skaler çarpimi, skaler bir büyüklüktür.
Vektörlerin Toplanması
Vektörel Büyüklükleri Toplamak için Üç Yöntem Kullanılır
1-) Paralel Kenar Yöntemi
Paralel kenar yöntemi iki vektörün birbiri ile toplanması için kullanılabilir. Bu yöntemde iki vektörün baslangıc noktaları birleştirilir, birinci vektörün baslangıç noktasından ikinci ve vektöre paralel ve eşit hayali bir vektör çizilir, aynı şekilde ikinci vektörden birinci vektöre eşit ve paralel hayali bir vektör çizilir. Daha sonra ilk vektörlerin kesisim noktası ile hayali vektörlerin kesisim noktası birleştirilerek yeni bir vektör elde edilir. Bu yeni vektör, ilk iki vektörün toplamidir ve yönü ilk vektörlerin kesisim noktasindan hayali vektörlerin kesisim noktasına dogrudur.Bu yöntemle elde edilen vektörü matematiksel olarak asağıdaki gibi göstere biliriz.
2-) Ucuca Ekleme Yöntemi
Ucuca ekleme yöntemi iki yada daha fazla vektörün toplanmasi için kullanilabilir. Bu yöntemde vektörlerden herhangi biri alinarak bitis noktasina diger bir vektör yerlestirilir, daha sonra baska bir vektör ise yerlestirilen bu yeni vektörün bitis noktasina yerlestirilir yani vektörler ucuca eklenir. Bu islem vektör sayisi kadar tekrarlanir. Ucuca ekleme işlemi tamamlandıktan sonra kullanilan ilk vektörün baslangiç noktasindan en son eklenen vektörün bitis noktasina dogru bir vektör çizilir. Elde edilen bu vektör ucuca eklenen vektörlerin toplamidir ve yönü kullanılan ilk vektörün başlanğıç noktasindan kullanilan son vektörün bitis noktasina dogrudur.
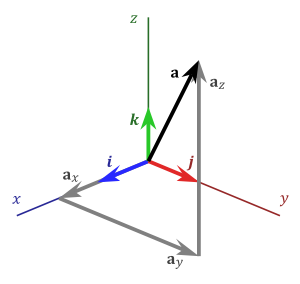
3-) Bileşenlerine Ayırma Yöntemi
Bilesenlerine ayirma yöntemi iki yada daha fazla vektörün toplanması için kullanılabilir. Bu yöntemde toplanacak tüm vektörler bir dik koordinatlar sistemine tasinir ve baslangiç noktalari koordinat sisteminin merkezine(orjine) gelecek sekilde yerlestirilir. Her bir vektörden “x” ve “y” düzlemlerine dikmeler indirilir. Indirilen dikmeler ile baslangiçtaki vektörlere ait “x” ve “y” bilesen vektörleri elde edilir.
Rx = R x cosµ
Ry = R x sinµ
Daha sonra elde edilen bu yeni vektörler birbirleri ile toplanir (Ters yönlü vektörler birbirini götürür).
Vektörlerde Çıkarma
Vektörlerde çikarma islemi yapilirken iki yol izlenebilir.
A-)Yöntem
Bu yöntemde ilk olarak çikarilacak olan vektör ters çevrilir, daha sonra ise olusan bu yeni vektör ile diger vektör ucuca ekleme yöntemi ile toplanirlar. ikiden fazla vektör kullanildiginda çikarilacak olan vektörler ters çevrilir toplanacak olanlar ise oldugu gibi birakilir ve ucuca toplama yöntemi ile toplama yapilir.
B-) Yöntem
Bu yöntemde iki vektör baslangiç noktalari birbiri ile çakisacak sekilde yan yana getirilir. Bu islemden sonra yönü, çikartilacak olan vektörün bitis noktasindan ilk vektörün bitis noktasina dogru olan bir vektör çizilir, böylece iki vektör birbirinden çikarilmis olur.